Cours Analyse 1 M. VALLET
Résumé de section
-
Ce cours représente 4 ECTS pour 20h de cours et 20h de TD. Son évaluation est en contrôle continu.
Son programme, qui s'inspire fortement du cours téléchargeable en ligne http://exo7.emath.fr/cours/livre-analyse-1.pdf, est :
1. Ensemble des entiers naturels, raisonnement par récurrence, notations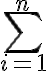 et
et 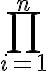 .
.
2. Propriétés fondamentales de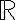 :
:
(a) valeur absolue, résolution d’inégalités mettant en jeu la valeur absolue, inégalité triangulaire.
(b) majorant, minorant, maximun, minimum, borne supérieure et inférieure, intervalle, segment.
(c) Théorème de la borne inférieure (admis).
3. Suites réelles
(a) Suites arithmétiques, géométriques, arithmético-géométriques, formules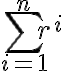 ,
, 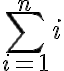
(b) Suites bornées, monotones, croissantes, décroissantes,
(c) Limite des suites réelles
i. Définition, suites convergentes, divergentes, suite tendant vers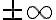 , unicité de la limite, convergente
implique bornée, rappel croissances comparées
, unicité de la limite, convergente
implique bornée, rappel croissances comparées
ii. opérations algébriques, compatibilité avec la relation d’ordre
iii. Théorèmes d’existence de la limite : encadrement, croissante et majorée, suites adjacentes
4. Fonctions réelles de la variable réelle
(a) Ensemble de définition, parité, imparité, croissance, décroissance, monotonie
(b) Limite en un point,
i. Unicité de la limite, limite à droite et à gauche, extension en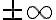
ii. Théorème d’existence de limite : toute fonction monotone sur![]a,b[ ]a,b[](https://elearn.univ-pau.fr/filter/tex/pix.php/e46b2a760c57eb995b62bd166b835b1e.gif) admet des limites à droite et à gauche en tout point
intérieur, discussion en
admet des limites à droite et à gauche en tout point
intérieur, discussion en 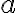 et
et 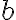
(c) Continuité :
i. Définition séquentielle, prolongement par continuité, continuité par morceaux
ii. Théorème des valeurs intermédiaires, l’image par une fonction continues d’un intervalle, (segment) est un intervalle (segment)
iii. Extrema : intervalles ouverts et segment
(d) Dérivabilité :
i. Définition, dérivées à droite et à gauche, linéarité, dérivée d’un produit, d’une composée
ii. Rappels : calculs de dérivées des fonctions usuelles, lien signe de la dérivée et sens de variations, tableau de variation
iii. Extrema : condition d’ordre 1 y compris aux bornes d’un segment
iv. Théorème des accroissements finis et inégalité des accroissements finis
v. Dérivées successives, formule de Leibniz, la dérivée d’ordre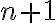 d’un polynôme de degré
d’un polynôme de degré 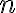 est nulle.
est nulle.
(e) Les fonctions usuelles : logarithme, puissances et exponentielle, fonction circulaires et hyperboliques, et leurs réciproques.
